Полые молекулы

Существует любопытный разрыв между значениями плотности газов (порядка 0,001 г/см³), с одной стороны, и жидкостей и твердых тел (от 0,5 до 25 г/см³) — с другой. Размышляя над тем, как заполнить этот разрыв, Дедал пришел к идее полой молекулы. Такая молекула могла бы представлять собой замкнутую сферическую оболочку плоской полимерной молекулы, подобной «молекуле» графита, имеющей плоскую гексагональную структуру — нечто вроде сетки с шестиугольными ячейками. Дедал предлагает модифицировать процесс высокотемпературного синтеза графита путем введения соответствующих примесных атомов или молекул, что вызвало бы изгиб плоской структуры (подобным образом с помощью примесей добиваются нужной структуры полупроводникового кристалла). Искривление плоского листа в конечном счете приведет к смыканию растущих краев и образованию замкнутой поверхности. Радиус пустотелой молекулы будет зависеть от количества введенной примеси. По расчетам Дедала, вещество, состоящее из полых молекул радиусом 0,05 мкм, будет иметь плотность около 0,04 г/см³, т. е. что-то среднее между плотностью жидкости и плотностью газа; такое вещество можно рассматривать как некое «пятое состояние» вещества. Эти гигантские молекулы (с молекулярной массой до 100 млн. единиц) едва ли способны «испаряться», а взаимодействовать между собой они будут так слабо, что подобное «состояние» вещества нельзя будет отнести ни к газообразному, ни к жидкому. Скорее всего, его можно рассматривать как «разреженную» жидкость, не улетучивающуюся из открытого сосуда, но и не принимающую его форму; при нагревании это вещество будет расширяться и переходить (не закипая) в газообразное состояние.

Столь замечательные вещества, безусловно, найдут множество применений — они открывают путь к созданию новых конструкций барометров и автомобильных амортизаторов, к новым принципам ожижения; вероятно, они окажутся идеальными смазочными материалами, обладающими, помимо ничтожно малой вязкости, еще и «эффектом шарикоподшипника». Вначале Дедал беспокоился, что внешние нагрузки приведут к деформации этих молекул, но затем понял, что, если их синтезировать в нормальной атмосфере, они будут упругими, как крошечные мячики. Теперь Дедал ищет способ оставлять в оболочках этих молекул небольшие «окошки», благодаря чему они могли бы поглощать молекулы внешней среды или обмениваться своим содержимым со средой, действуя как исключительно эффективные молекулярные сита. Таким образом, они могли бы накапливать внутри себя молекулы внешней сферы в количестве, в сотни раз превышающем их собственный вес.

New Scientist, November 3, 1966

Будет ли полая молекула стабильной? Есть вероятность, что под внешним воздействием она легко деформируется и «сплющится», изменив свою форму примерно так, как показано на рисунке.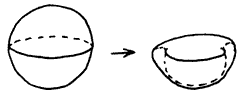

Чтобы молекула была устойчива и не подвергалась такому «выворачиванию», энергия, соответствующая сближению двух полушарий молекулы, должна быть меньше энергии, необходимой для образования экваториального перегиба. Попробуем оценить величину каждой из этих энергий.

а. Сила, необходимая для поворота химической связи на угол θ относительно равновесного положения, равна krθ, где r — длина связи, k — константа жесткости химической связи, а соответствующее значение энергии равно 1/2k(rθ)². Чтобы «вывернуть» полую молекулу, необходимо повернуть все связи вдоль «экватора» на 180°, или π радиан. При длине «экватора» 2πR (где R — радиус молекулы) и расстоянии между отдельными атомами r (длина связи между атомами в плоской решетке) число повернутых связей составляет 2πR/r, а необходимая для «выворачивания» молекулы энергия равна E_выв = (2πR/r) × (1/2kr²π²) = π³kRr.

б. Высвобождение энергии при сплющивании молекулы обусловлено уменьшением свободной поверхности молекулы на величину 4πR² при слиянии двух полушарий; таким образом, E_пов = 4πR²γ, где γ — удельная поверхностная энергия. Как можно было предвидеть, поверхностная энергия E_пов, способствующая сплющиванию молекулы, увеличивается пропорционально R², в то время как энергия, необходимая для выворачивания молекулы, E_выв, пропорциональна первой степени R. Поэтому с увеличением радиуса молекулы E_пов на каком-то этапе неизбежно превысит E_выв — и молекула сплющится. Предел устойчивости соответствует случаю, когда E_пов = E_выв, так что максимальный радиус молекулы получим, приравняв выражения для названных энергий: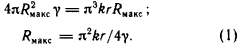

(Наши рассуждения, конечно, не слишком строги. При выворачивании молекулы будет поворачиваться не одна связь на «экваторе» на 180°, а несколько последовательно расположенных связей повернутся на меньший угол, что приведет к уменьшению полной энергии выворачивания. С другой стороны, в образующейся экваториальной «впадине» сохранится свободная поверхность, следовательно, высвобождается не вся поверхностная энергия. Эти два эффекта взаимно компенсируются, так что результирующая ошибка может быть не слишком большой.)

Подставим в уравнение (1) соответствующие численные значения, характерные для кристаллической решетки графита: r = 1,4×10^-10 м, k = 20 Н/м (эти значения получены для бензольного кольца, которое в некотором смысле можно рассматривать как единичную ячейку гексагональной решетки графита); γ = 0,3 Дж/м (по грубой оценке, сделанной для плоской чешуйки графита). Тогда находим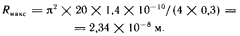

Получается, что наша полая молекула имеет в поперечнике 0,05 мкм — примерно 330 диаметров атома! Такая молекула будет состоять примерно из 260 000 атомов углерода, а ее масса достигнет 12×260000 = 3,1×10⁶ единиц. Считая, что каждая молекула занимает объем, равный примерно кубу со стороной 5×10^-8 м, мы получим плотность нашего «вещества»: масса/объем = (3,1×10⁶ × 1,67×10^-27)/(5×10^-8)3 = 40 кг/м³. Вещество оказывается очень легким — в 25 раз легче воды. Вероятно, можно получить полые молекулы и большего размера, так что плотность вещества не превысит 5 кг/м³, а молекулярная масса достигнет сотен миллионов единиц, однако, чтобы обеспечить устойчивость таких молекул, придется внутри их поддерживать избыточное давление газа.

Теория многогранных молекул. Согласно теореме Эйлера, у любого многогранника (число вершин) + (число граней) – (число ребер) = 2 (В + Г – Р = 2). В силу этой теоремы невозможно построить многогранник с шестиугольными гранями, поскольку в этом случае было бы В + Г – Р = 0. В своей замечательной книге «Рост и форма» (Growth and Form, Cambridge University Press, p. 708, 738) Д'Арси Томпсон рассматривает эту задачу в применении к радиоляриям — микроскопическим морским обитателям, чьи известковые скелеты нередко имеют вид гексагональной сетки. Даже восхитительная в своей симметричности Aulonia hexagona (которую можно было бы рассматривать как увеличенное в 105 раз изображение полой графитовой молекулы, состоящей из 1200 атомов) имеет несколько нешестиугольных граней: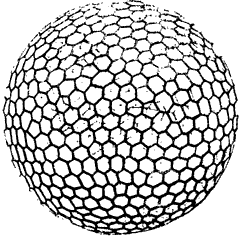

Aulonia hexagona; увеличение примерно 200 крат (из книги Д'Арси Томпсона «Рост и форма»; с разрешения изд-ва «Кембридж юниверсити пресc).

Томпсон показывает, что гексагональную сетку произвольной величины можно замкнуть в многогранник[27], включив в нее ровно 12 пятиугольников. Поэтому если для сворачивания решетки графита в сферу использовать примеси, вызывающие образование пятиугольных ячеек в гексагональной сетке, то понадобится ровно 12 атомов примеси на то число атомов графита, которое содержится в одной полой молекуле. Например, для самых больших молекул, состоящих из 260000 атомов графита, потребуется вводить примесь в количестве 12/260000 = 46 молярных долей на миллион. Это значительная концентрация примесей по сравнению с тем количеством примесей, которое обычно вводят в полупроводники.

Комментарий Дедала

Со времени опубликования моего предложения химия полых молекул не продвинулась сколько-нибудь заметно. Рекордом в химии углеводородов можно считать синтез молекулы, представляющей собой двенадцатигранник с пятиугольными гранями (Science, 211, 1981, р. 575). Так держать, ребята!

Примечания:

2

Интересно, что появление газовых включений в твердом теле подсказано природой. Газовые включения (окклюзии) часто наблюдаются в кварце или янтаре (см. [1]). — Прим. ред.

27

Молекулы, имеющие форму широкого кольца и обладающие высокоизбирательной поглощающей способностью по отношению к катионам («краун»-эфиры), широко используются на практике; см. ([20], с. 460 [21]). — Прим. ред.